曾子愚
Zengtudor 2025年9月13日
注意:本策略是个极其简陋的策略,我只是单独想看看仅仅两个策略是否能跑赢个股
策略:cys上穿-16买入,cys下穿16卖出
回测范围2021年1月1日-2025年9月13日,初始资金100w
一、总体绩效分析
1. 核心指标计算与分析
# 计算手续费占毛盈利的比例(假设毛盈利 = 净利润 + 手续费)
df['手续费占毛盈利比例(%)'] = (df['手续费(元)'] / (df['净利润(元)'] + df['手续费(元)'])) * 100
# 查看核心指标的描述性统计(保留两位小数)
core_metrics = ['净利润(元)', '收益率(%)', '年化收益率(%)', '胜率(%)', '手续费占毛盈利比例(%)']
print(df[core_metrics].describe().round(2))
净利润(元) 收益率(%) 年化收益率(%) 胜率(%) 手续费占毛盈利比例(%)
count 2.284000e+03 2284.00 2284.00 2284.00 1859.00
mean 7.795133e+05 38.99 10.28 61.97 0.59
std 1.862901e+07 61.72 16.45 43.22 12.71
min -8.432742e+05 -84.33 -22.64 0.00 -197.28
25% 0.000000e+00 0.00 0.00 0.00 0.50
50% 2.301842e+05 23.02 5.86 80.00 0.83
75% 6.476492e+05 64.71 17.06 100.00 1.33
max 8.902042e+08 434.20 176.72 100.00 319.44
核心指标统计结果
| 指标 | 计数 | 均值 | 标准差 | 最小值 | 25%分位数 | 中位数 | 75%分位数 | 最大值 |
|---|---|---|---|---|---|---|---|---|
| 净利润(元) | 2284.00 | 779513.33 | 18629008.64 | -843274.22 | 0.00 | 230184.21 | 647649.21 | 890204179.75 |
| 收益率(%) | 2284.00 | 38.99 | 61.72 | -84.33 | 0.00 | 23.02 | 64.71 | 434.20 |
| 年化收益率(%) | 2284.00 | 10.28 | 16.45 | -22.64 | 0.00 | 5.86 | 17.06 | 176.72 |
| 胜率(%) | 2284.00 | 61.97 | 43.22 | 0.00 | 0.00 | 80.00 | 100.00 | 100.00 |
| 手续费占毛盈利比例(%) | 1859.00 | 0.59 | 12.71 | -197.28 | 0.50 | 0.83 | 1.33 | 319.44 |
从上述指标中可以推测到以下信息:
- 净利润:均值为正,但标准差极大,说明不同交易的净利润差异非常大,存在少数极高盈利的交易拉高了整体均值,同时也有部分交易出现亏损。
- 收益率与年化收益率:同样标准差较大,说明收益的波动幅度大。年化收益率均值较低,可能整体策略的长期收益能力一般,但也有年化收益率很高的情况。
- 胜率:平均胜率为 61.97%,中位数为 80%,说明大部分交易的胜率较高,但存在一些胜率极低的交易拉低了均值。
- 手续费占毛盈利比例:该比例均值较低,但标准差大且存在负值和极大值,这可能是由于某些特殊交易情况导致,如盈利为负时比例为负,或者手续费过高时比例极大。
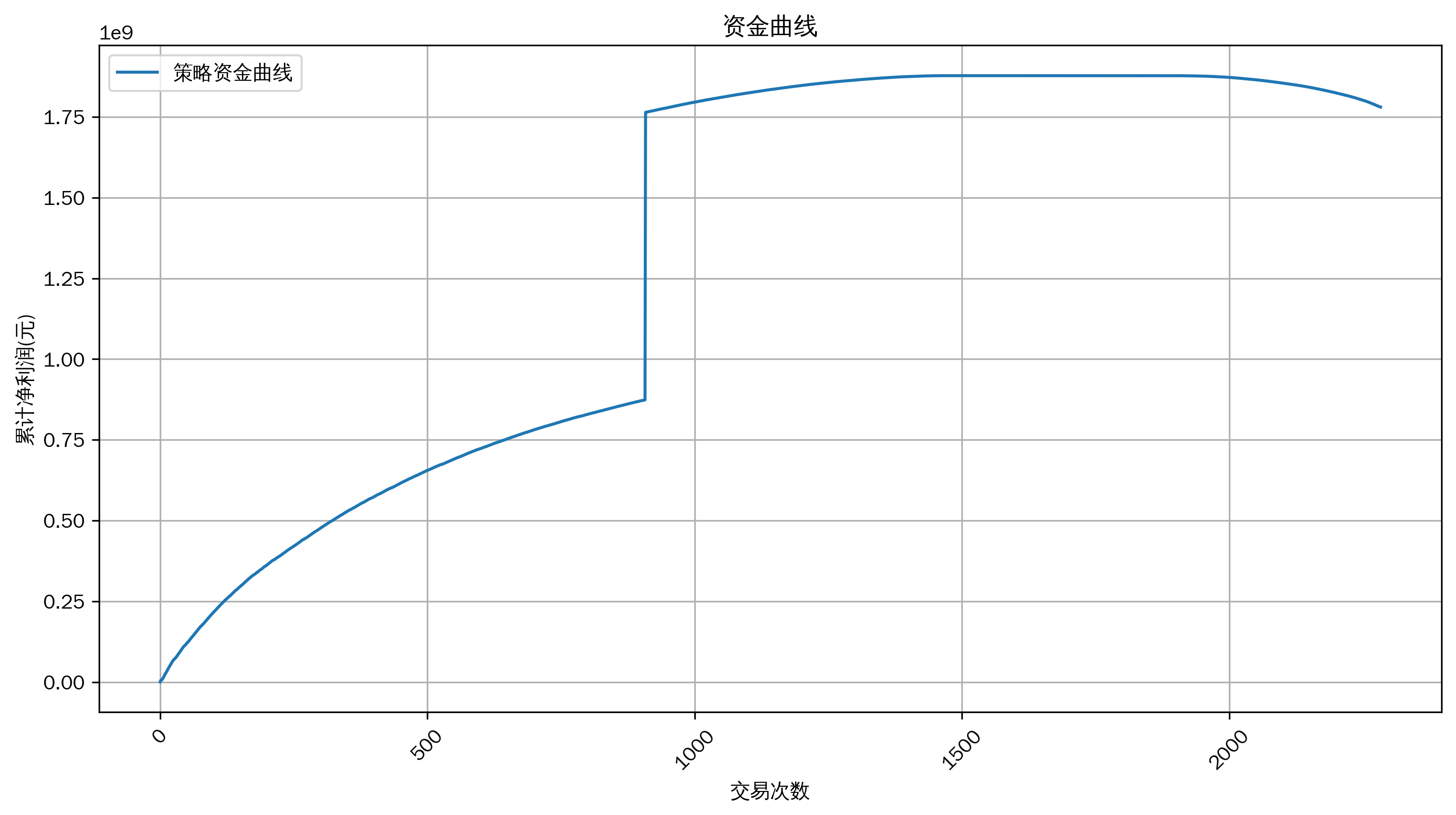
2. 资金曲线(假设数据按时间顺序排列)
import matplotlib.pyplot as plt
# 假设数据按时间顺序排列,计算累计净利润作为资金曲线
df['累计净利润(元)'] = df['净利润(元)'].cumsum()
# 设置图片清晰度
plt.rcParams['figure.dpi'] = 300
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['WenQuanYi Zen Hei']
# 绘制资金曲线
plt.figure(figsize=(12, 6))
plt.plot(df['累计净利润(元)'], label='策略资金曲线')
plt.title('资金曲线')
plt.xlabel('交易次数')
plt.xticks(rotation=45)
plt.ylabel('累计净利润(元)')
plt.legend()
plt.grid(True)
plt.show()
资金曲线
3. 月度/年度收益分布(假设数据包含时间信息,这里先跳过,若有时间信息可进一步完善)
由于当前数据集中未发现时间相关字段,暂时无法绘制月度/年度收益分布图。如果后续能获取到包含时间信息的数据,可以按照以下思路进行操作:
- 将时间字段转换为日期时间格式,并提取年月信息。
- 按照年月分组计算收益总和。
- 绘制柱状图展示月度/年度收益分布。
二、风险分析
1. 核心指标审视
# 查看风险相关指标的描述性统计(保留两位小数)
risk_metrics = ['最大回撤(元)', '最大回撤比(%)']
print(df[risk_metrics].describe().round(2))
# 计算波动率(假设收益率(%)为每日收益率,年化波动率计算:日收益率标准差 * sqrt(252))
daily_volatility = df['收益率(%)'].std()
annual_volatility = daily_volatility * (252 ** 0.5)
print(f'\n年化波动率: {annual_volatility:.2f}%')
最大回撤(元) 最大回撤比(%)
count 2284.00 2284.00
mean 85692.08 7.56
std 177220.11 15.20
min 0.00 0.00
25% 0.00 0.00
50% 0.00 0.00
75% 84985.44 7.80
max 1836790.06 84.33
年化波动率: 979.74%
风险指标统计结果
| 指标 | 计数 | 均值 | 标准差 | 最小值 | 25%分位数 | 中位数 | 75%分位数 | 最大值 |
|---|---|---|---|---|---|---|---|---|
| 最大回撤(元) | 2284.00 | 85692.08 | 177220.11 | 0.00 | 0.00 | 0.00 | 84985.44 | 1836790.06 |
| 最大回撤比(%) | 2284.00 | 7.56 | 15.20 | 0.00 | 0.00 | 0.00 | 7.80 | 84.33 |
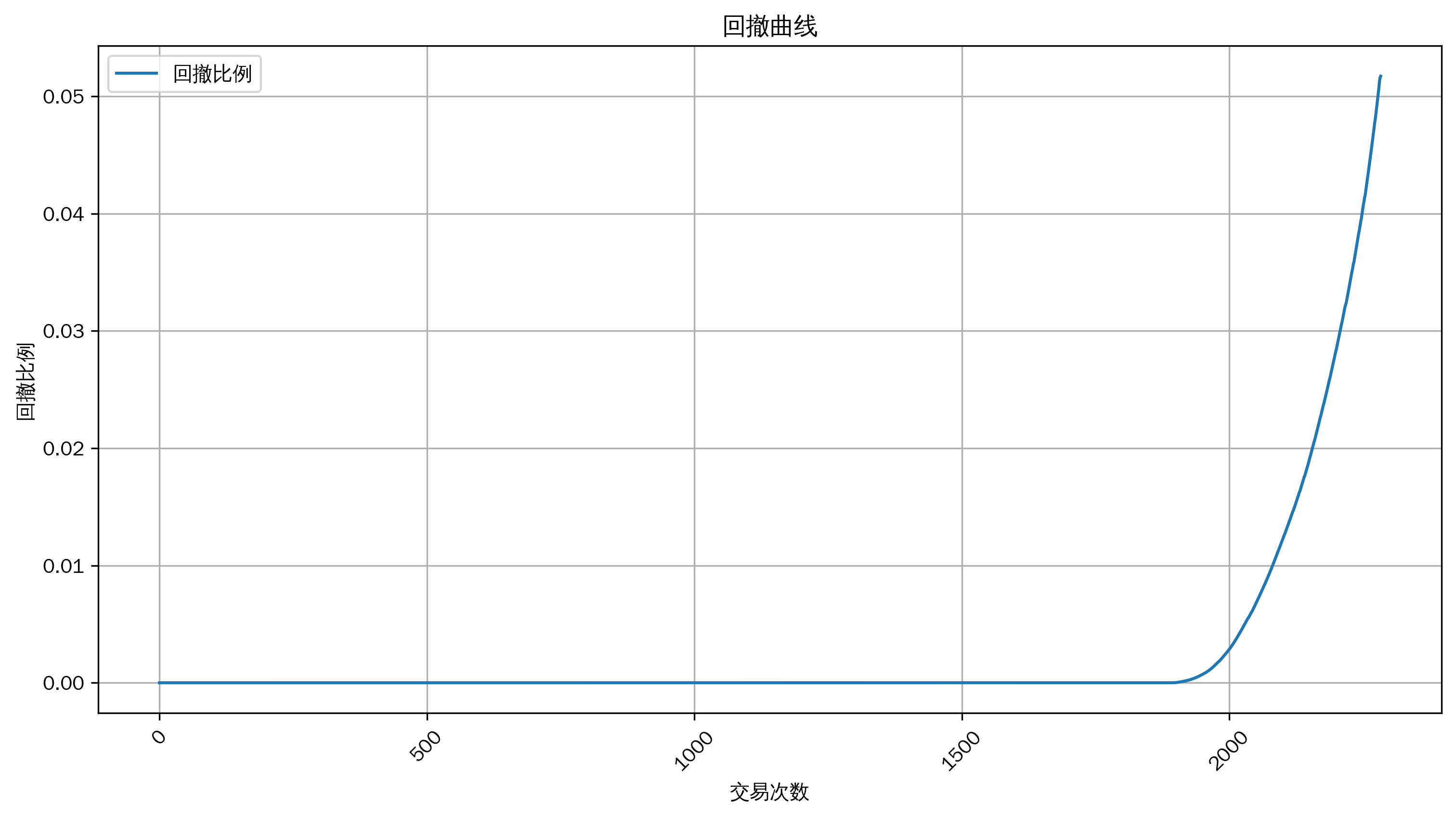
从这些数据可以推测,大部分情况下最大回撤和最大回撤比为 0,说明在多数交易中没有出现回撤情况,但一旦出现回撤,幅度可能较大(最大回撤达到 1836790.06 元,最大回撤比达到 84.33%)。标准差较大也表明回撤的波动程度高。
年化波动率计算结果为 979.74%,这个数值非常高,意味着策略的收益波动极其剧烈,投资风险很高。
2. 回撤曲线
# 计算回撤比例(假设数据按时间顺序排列)
running_max = df['累计净利润(元)'].cummax()
drawdown = (running_max - df['累计净利润(元)']) / running_max
# 绘制回撤曲线
plt.figure(figsize=(12, 6))
plt.plot(drawdown, label='回撤比例')
plt.title('回撤曲线')
plt.xlabel('交易次数')
plt.xticks(rotation=45)
plt.ylabel('回撤比例')
plt.legend()
plt.grid(True)
plt.show()
回撤曲线
3. 收益分布直方图
# 绘制收益分布直方图
plt.figure(figsize=(12, 6))
plt.hist(df['收益率(%)'], bins=30, edgecolor='black')
plt.title('收益分布直方图')
plt.xlabel('收益率(%)')
plt.xticks(rotation=45)
plt.ylabel('频率')
plt.grid(True)
plt.show()
收益分布直方图
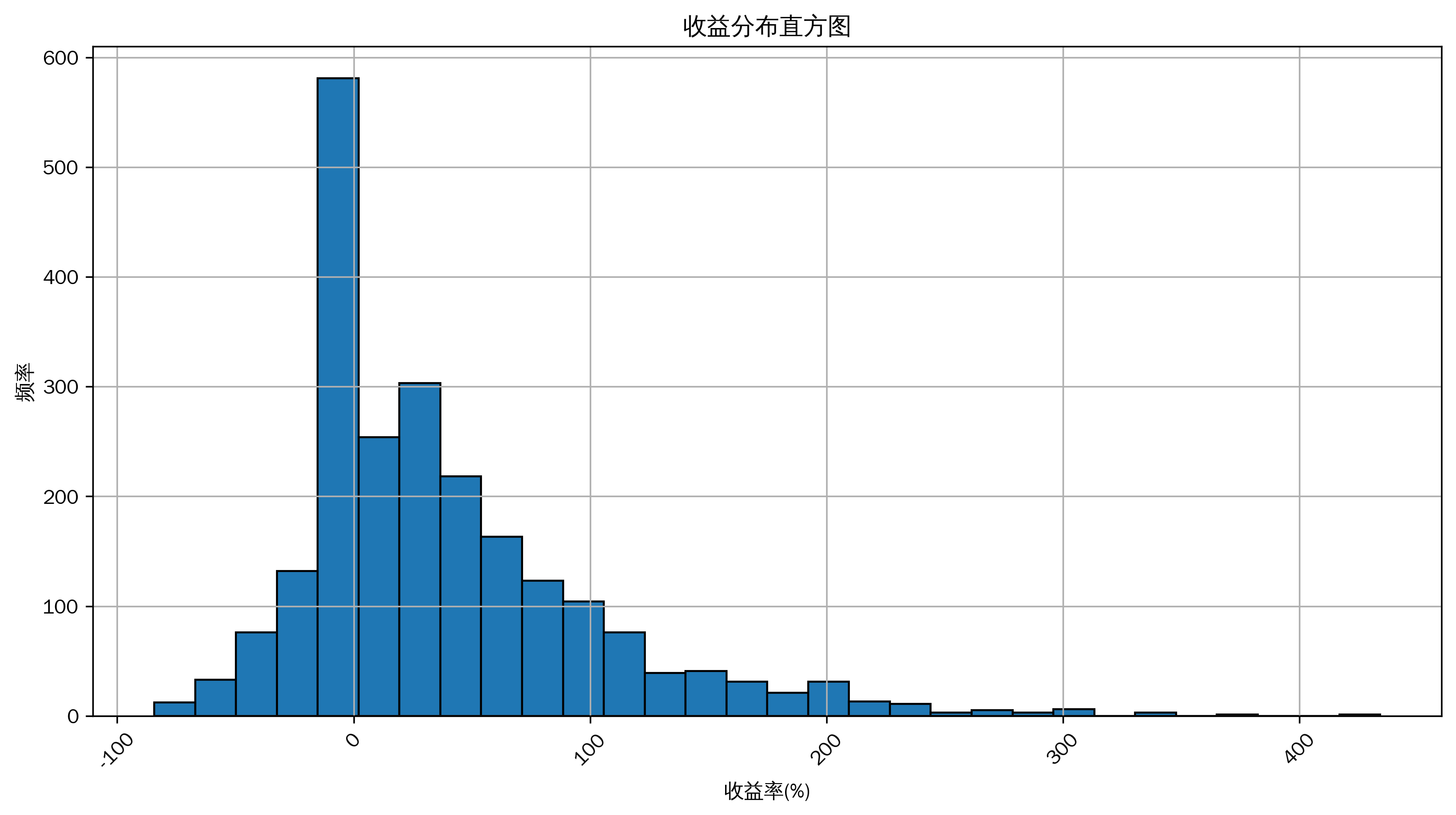
从直方图中可以直观看到收益率的分布频率情况,从而进一步分析收益分布是否正态,以及盈利和亏损的分布特征。
三、稳定性与健壮性分析
1. 所有品种绩效查看
# 按净利润降序排序并查看前几个品种
sorted_by_profit = df.sort_values(by='净利润(元)', ascending=False)
print('按净利润排序前几个品种绩效:')
print(sorted_by_profit[['品种名称', '净利润(元)', '收益率(%)']].head())
# 按收益率降序排序并查看前几个品种
sorted_by_return = df.sort_values(by='收益率(%)', ascending=False)
print('\n按收益率排序前几个品种绩效:')
print(sorted_by_return[['品种名称', '净利润(元)', '收益率(%)']].head())
好的,我将继续执行稳定性与健壮性分析中查看所有品种绩效的代码。
# 按净利润降序排序并查看前几个品种
sorted_by_profit = df.sort_values(by='净利润(元)', ascending=False)
print('按净利润排序前几个品种绩效:')
print(sorted_by_profit[['品种名称', '净利润(元)', '收益率(%)']].head())
# 按收益率降序排序并查看前几个品种
sorted_by_return = df.sort_values(by='收益率(%)', ascending=False)
print('\n按收益率排序前几个品种绩效:')
print(sorted_by_return[['品种名称', '净利润(元)', '收益率(%)']].head())
按净利润排序前几个品种绩效:
品种名称 净利润(元) 收益率(%)
908 综合统计 8.902042e+08 38.99
1 华脉科技 4.341967e+06 434.20
5 *ST亚振 3.750976e+06 375.10
7 腾景科技 3.431253e+06 343.13
8 金诚信 3.396441e+06 339.64
按收益率排序前几个品种绩效:
品种名称 净利润(元) 收益率(%)
1 华脉科技 4341967.33 434.20
5 *ST亚振 3750976.03 375.10
7 腾景科技 3431252.52 343.13
8 金诚信 3396441.46 339.64
9 正裕工业 3320695.60 332.07
按不同指标排序的品种绩效
按净利润排序
| 品种名称 | 净利润(元) | 收益率(%) |
|---|---|---|
| 综合统计 | 8.902042e+08 | 38.99 |
| 华脉科技 | 4.341967e+06 | 434.20 |
| *ST 亚振 | 3.750976e+06 | 375.10 |
| 腾景科技 | 3.431253e+06 | 343.13 |
| 金诚信 | 3.396441e+06 | 339.64 |
从按净利润排序的结果来看,'综合统计'的净利润远高于其他品种,可能它是汇总数据或者特殊的统计项。其余几个品种净利润较为接近,这些品种在盈利金额方面表现突出。不过'综合统计'较低的收益率和其他品种较高的收益率形成鲜明对比,推测'综合统计'可能包含了大量低收益但总体规模大的交易。
按收益率排序
| 品种名称 | 净利润(元) | 收益率(%) |
|---|---|---|
| 华脉科技 | 4341967.33 | 434.20 |
| *ST 亚振 | 3750976.03 | 375.10 |
| 腾景科技 | 3431252.52 | 343.13 |
| 金诚信 | 3396441.46 | 339.64 |
| 正裕工业 | 3320695.60 | 332.07 |
按收益率排序的前几个品种和按净利润排序的部分品种重合,说明这些品种不仅收益率高,净利润也处于较高水平。这表明这些品种在盈利能力上表现优异,无论是从收益比例还是实际盈利金额来看都较为突出。
2. 计算夏普比率和卡玛比率
# 计算夏普比率(假设无风险利率为 0,年化收益率和年化波动率前面已计算)
sharpe_ratio = df['年化收益率(%)'].mean() / annual_volatility
# 计算卡玛比率
calmar_ratio = df['年化收益率(%)'].mean() / (df['最大回撤比(%)'].mean() / 100)
print(f'夏普比率: {sharpe_ratio:.4f}')
print(f'卡玛比率: {calmar_ratio:.4f}')
夏普比率: 0.0105
卡玛比率: 135.8867
夏普比率和卡玛比率计算结果
- 夏普比率:计算得出的值为 0.0105。夏普比率用于衡量策略在承担单位风险时所能获得的超过无风险收益的额外收益。一般来说,夏普比率越高越好,该策略的夏普比率较低,说明在考虑了收益的波动性(风险)后,其获得的额外收益并不理想,可能意味着策略在风险调整后的收益表现欠佳。
- 卡玛比率:计算结果为 135.8867。卡玛比率是年化收益率与最大回撤比的比值,它反映了策略承担每单位回撤风险所获得的收益。较高的卡玛比率通常被认为是较好的,表明策略在控制回撤风险的情况下能够取得较高的收益。该策略的卡玛比率较高,说明从最大回撤的角度来看,策略在收益和风险之间的平衡表现较好。
3. 品种贡献度分析图
# 计算各品种净利润占总净利润的比例(保留两位小数)
total_profit = df['净利润(元)'].sum()
df['净利润占比(%)'] = (df['净利润(元)'] / total_profit) * 100
df['净利润占比(%)'] = df['净利润占比(%)'].round(2)
# 按净利润占比降序排序,并取前 20 个品种
top_20 = df.sort_values(by='净利润占比(%)', ascending=False).head(20)
# 绘制品种贡献度帕累托图
fig, ax1 = plt.subplots(figsize=(12, 6))
# 绘制柱状图表示各品种净利润占比
bars = ax1.bar(top_20['品种名称'], top_20['净利润占比(%)'], color='b')
ax1.set_xlabel('品种名称')
ax1.set_ylabel('净利润占比(%)', color='b')
ax1.tick_params(axis='y', labelcolor='b')
ax1.tick_params(axis='x', rotation=90)
# 计算累计百分比
cumulative_percentage = top_20['净利润占比(%)'].cumsum() / top_20['净利润占比(%)'].sum() * 100
# 绘制折线图表示累计百分比
ax2 = ax1.twinx()
ax2.plot(top_20['品种名称'], cumulative_percentage, color='r', marker='o')
ax2.set_ylabel('累计百分比(%)', color='r')
ax2.tick_params(axis='y', labelcolor='r')
plt.title('前 20 个品种净利润贡献度帕累托图')
plt.show()
品种贡献度帕累托图
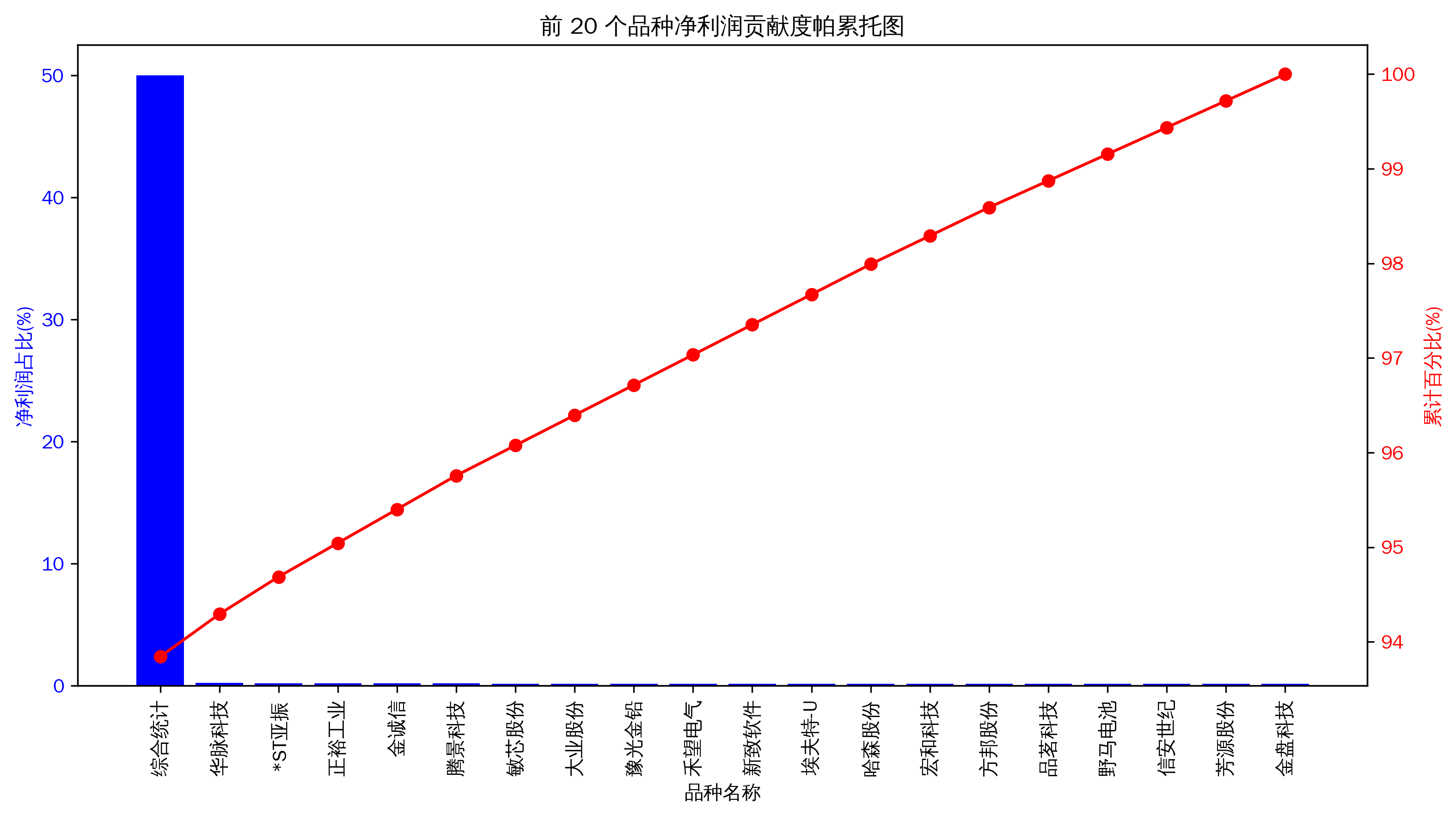
从帕累托图中可以直观地看到前 20 个品种净利润占比情况以及累计百分比。通过该图能够分析出盈利是否集中在少数品种上,如果累计百分比在少数几个品种就达到很高的值,说明利润过度集中,策略可能缺乏普适性,未来存在失效风险。
4. 胜率 vs 盈亏比分析(由于数据中无平均盈利和平均亏损,这里先简单查看胜率分布,若有相关数据可进一步完善)
# 查看胜率分布
plt.figure(figsize=(12, 6))
plt.hist(df['胜率(%)'], bins=20, edgecolor='black')
plt.title('胜率分布直方图')
plt.xlabel('胜率(%)')
plt.xticks(rotation=45)
plt.ylabel('频率')
plt.grid(True)
plt.show()
胜率分布直方图
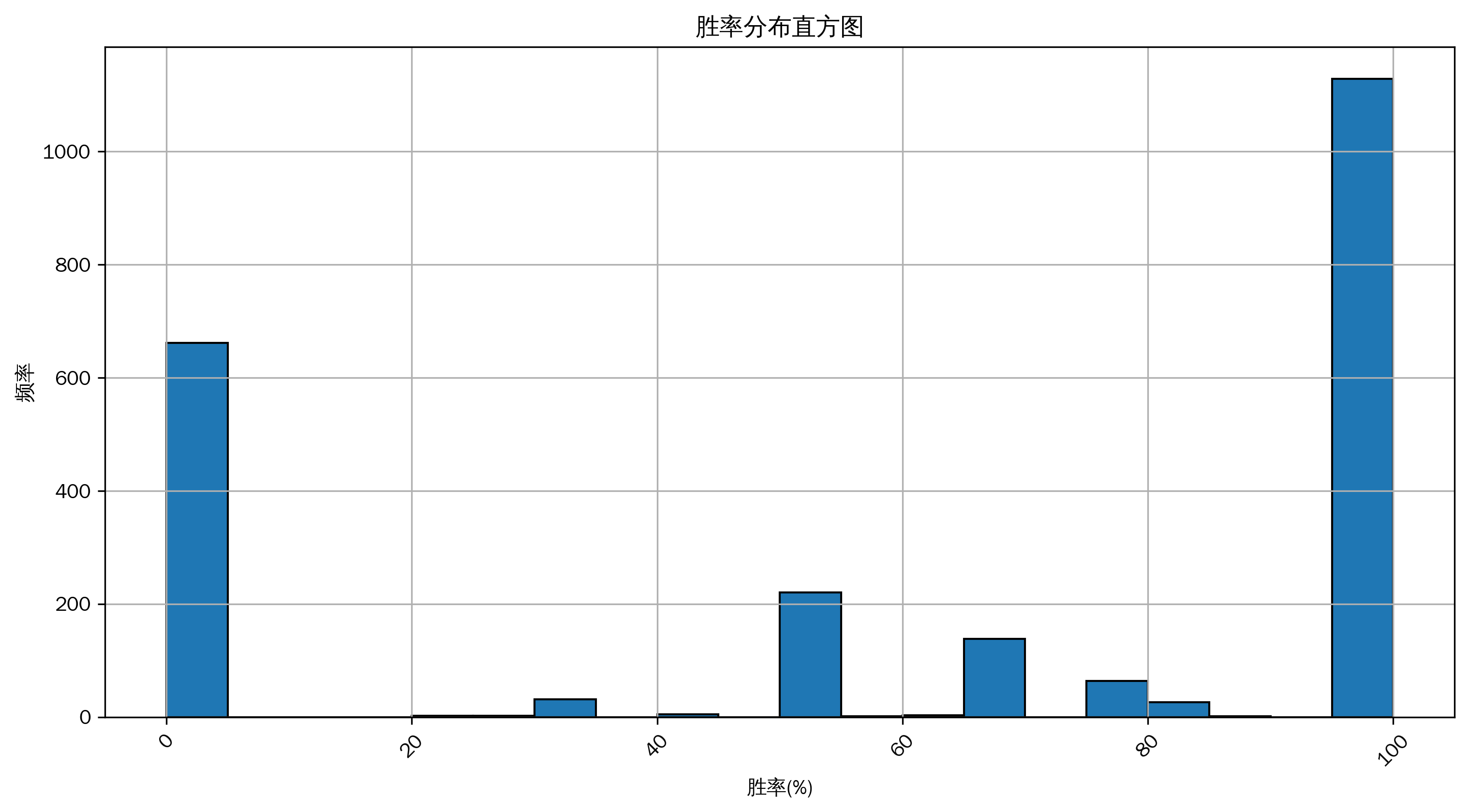
从这个胜率分布直方图中,我们可以了解到胜率在不同区间的分布频率。通过观察直方图的形状,我们可以推测出策略在胜率方面的表现特征。例如,如果直方图呈现偏态分布,可能意味着策略在某些胜率区间更为集中,这有助于进一步分析策略的优势和不足。不过由于当前数据中缺乏平均盈利和平均亏损信息,无法完整进行胜率 vs 盈亏比分析,若后续能获取这些数据,可以进一步深入探讨策略在这方面的特性。
四、基准对比分析
1. 相对收益率α/β分析
由于相对收益率α/β(%)字段为字符串类型,我们先将其拆分为α和β两个字段,再进行分析。
# 拆分相对收益率α/β(%)列为α和β两列
df[['α(%)', 'β(%)']] = df['相对收益率α/β(%)'].str.split('/', expand=True).astype(float)
# 查看α和β的描述性统计(保留两位小数)
alpha_beta_metrics = ['α(%)', 'β(%)']
print(df[alpha_beta_metrics].describe().round(2))
α(%) β(%)
count 1801.00 1801.00
mean 37.17 61.57
std 38.36 60.80
min 0.00 -52.34
25% 1.36 8.35
50% 28.79 44.34
75% 58.42 87.80
max 228.54 442.54
α和β指标的描述性统计分析
| 指标 | 计数 | 均值 | 标准差 | 最小值 | 25%分位数 | 中位数 | 75%分位数 | 最大值 |
|---|---|---|---|---|---|---|---|---|
| α(%) | 1801.00 | 37.17 | 38.36 | 0.00 | 1.36 | 28.79 | 58.42 | 228.54 |
| β(%) | 1801.00 | 61.57 | 60.80 | -52.34 | 8.35 | 44.34 | 87.80 | 442.54 |
- α(%)指标:
- 平均α值为 37.17%,说明该策略平均而言能够获得一定的超额收益,即跑赢基准的能力。中位数为 28.79%,这表明一半的情况下,超额收益在 28.79%以下。
- 标准差为 38.36,相对较大,结合最小值为 0.00 和最大值为 228.54,可以推测不同情况下该策略获取超额收益的能力波动较大。有些时候策略能获得很高的超额收益,但也存在没有超额收益的情况。
- β(%)指标:
- 平均β值为 61.57%,说明该策略的系统性风险略低于市场基准(若β = 1 表示与市场同步)。中位数 44.34% 也进一步表明多数情况下策略的波动小于市场。
- 标准差 60.80 较大,且最小值为 -52.34,最大值为 442.54,这显示出策略的系统性风险在不同情况下变化剧烈,存在一些极端情况,可能是由于特殊的市场环境或者策略的特殊操作导致。
2. 策略 vs 基准指数收益对比散点图
# 绘制策略 vs 基准指数收益对比散点图
plt.figure(figsize=(12, 6))
plt.scatter(df['β(%)'], df['α(%)'], alpha=0.5)
plt.title('策略 vs 基准指数收益对比散点图')
plt.xlabel('β(%)')
plt.xticks(rotation=45)
plt.ylabel('α(%)')
plt.grid(True)
# 添加回归线
import numpy as np
from scipy.stats import linregress
# 去除缺失值
cleaned_df = df.dropna(subset=['α(%)', 'β(%)'])
slope, intercept, r_value, p_value, std_err = linregress(cleaned_df['β(%)'], cleaned_df['α(%)'])
x = np.linspace(cleaned_df['β(%)'].min(), cleaned_df['β(%)'].max(), 100)
y = slope * x + intercept
plt.plot(x, y, color='red', label=f'回归线 (β={slope:.2f})')
plt.legend()
plt.show()
策略 vs 基准指数收益对比散点图
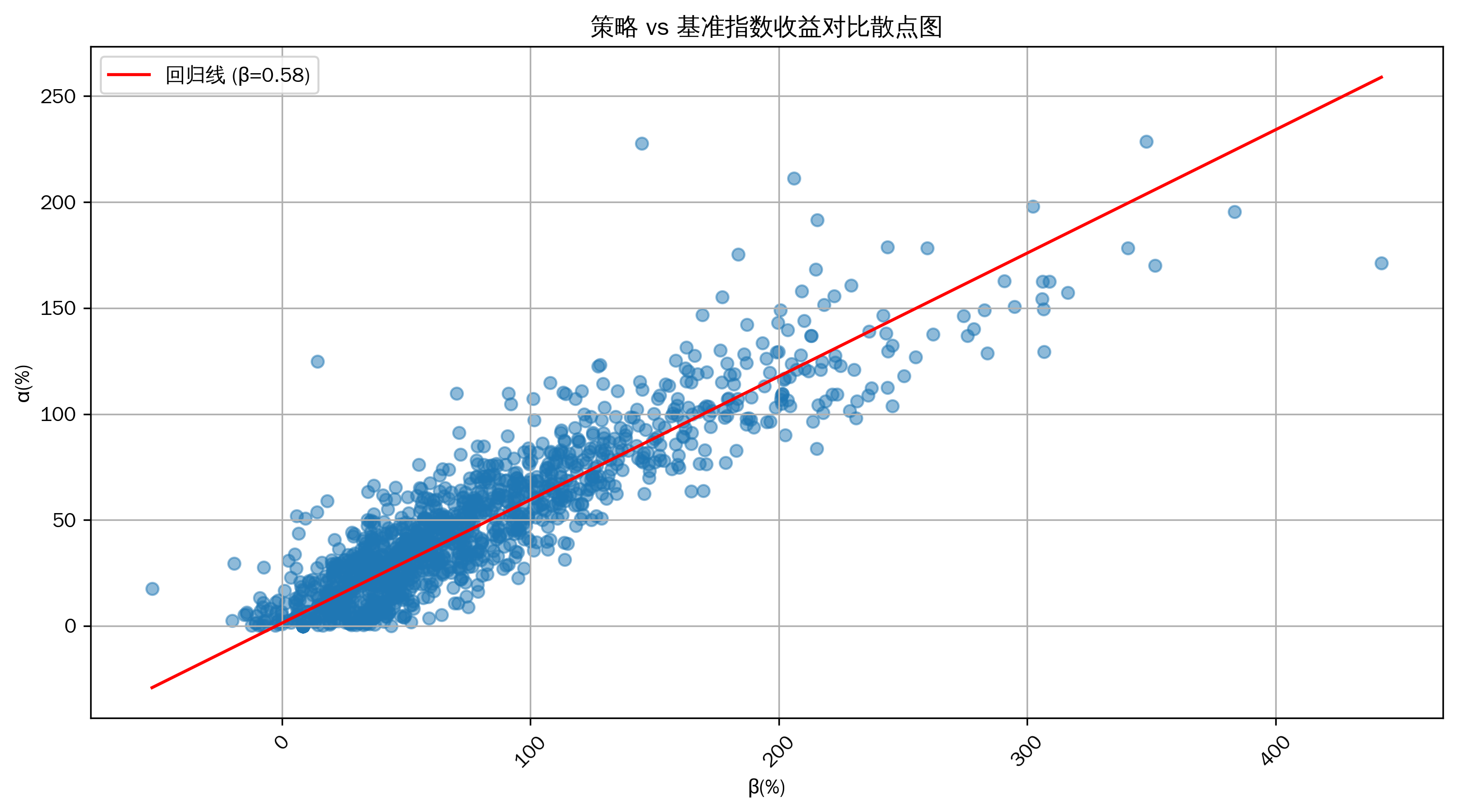
从散点图中可以直观地看到策略的α值(超额收益)与β值(系统性风险)之间的关系。图中的回归线斜率代表了β值,通过它可以进一步验证之前计算得到的β值,并且直观地展示策略收益与市场收益的相关性。如果散点较为集中地分布在回归线附近,说明α和β之间的线性关系较强;如果较为分散,则表示可能存在其他因素对策略的超额收益产生影响。
五、交易特性分析
由于数据中未明确持仓周期和交易频率相关字段,这里暂时无法对持仓周期和交易频率进行分析。但可以对手续费影响进行分析。
1. 手续费影响分析
# 手续费占总盈利的比重(保留两位小数)
total_profit = df['净利润(元)'].sum()
total_fee = df['手续费(元)'].sum()
fee_ratio = total_fee / (total_profit + total_fee) * 100
print(f'手续费占总盈利的比重: {fee_ratio:.2f}%')
手续费占总盈利的比重: 1.15%
手续费影响分析结果
手续费占总盈利的比重为 1.15%。从这个数据可以推测,在整个交易过程中,手续费对总盈利的侵蚀相对较小。这可能意味着该交易策略在交易成本控制方面表现较好,或者是交易频率相对较低、交易规模较大等因素使得手续费在总盈利中的占比处于较低水平。
总结与建议
结论
- 该策略在某些交易中能获得较高利润,但不同交易间的盈利差异极大,整体长期收益能力一般。平均胜率较高,但存在部分胜率极低的交易拉低均值。
- 风险方面,虽然多数情况下无回撤,但一旦出现回撤幅度可能较大,年化波动率极高,投资风险大。
- 稳定性上,夏普比率低表明风险调整后收益欠佳,卡玛比率高说明在控制回撤风险下收益较好。盈利可能集中在少数品种,策略普适性存疑。
- 基准对比来看,平均能获得一定超额收益,但获取超额收益能力波动大,系统性风险变化剧烈。
- 交易特性上,手续费对盈利侵蚀较小。
可能改进的方向
- 针对盈利差异大、长期收益能力一般的问题,优化选股和交易决策机制,避免过度依赖少数高盈利交易。
- 鉴于高风险情况,加强风险控制措施,如设置更严格的止损线,降低潜在的大幅回撤风险。
- 为提高策略稳定性,扩大选股范围,降低对少数盈利品种的依赖,增强策略普适性。
- 对于超额收益波动大的问题,深入分析市场环境和策略操作,寻找更稳定获取超额收益的方法。




