斐波那契数日

背景

今天是2024年11月23日，1123，是斐波那契数列的前几位，纪念一下

斐波那契递推式

• F_0=0

• F_1=1

• F_i=F_{i-1}+F_{i-2} (i\geq2)

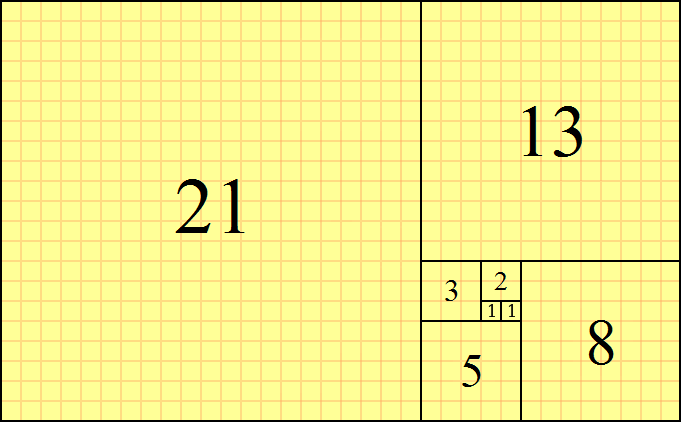
斐波那契数列是一种经典的数列，其定义是：每个数都是前两个数之和，通常以0和1作为起始数列的前两个数。斐波那契数列的常见形式为：

介绍

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

斐波那契数列在多个领域都有广泛的应用，主要包括：

1. 数学与计算机科学：斐波那契数列在算法分析中有重要应用，尤其是在递归算法、动态规划和数据结构（如斐波那契堆）中。

2. 最佳化问题：在一些最优选择问题中，斐波那契数列帮助构造递归关系，从而完成问题的优化。

3. 生物学：许多自然现象，例如植物的叶序、生物繁殖模式等，都可以用斐波那契数列来解释。例如，某些植物的果实和花瓣的排列数量常与斐波那契数相关。

4. 金融市场：技术分析中，斐波那契数列及其比例（如斐波那契回撤）被用于预测市场走势，帮助交易者识别支撑位和阻力位。

5. 艺术与设计：斐波那契数列与黄金比例关系密切，常用于建筑、绘画和其他视觉艺术中，以达到美学上的平衡和谐。

6. 音乐：在某些音乐作品中，斐波那契数列被用于调性、节奏及结构的设计。

7. 游戏开发：在某些算法中，斐波那契数列可以用于生成随机数、配置资源等。

总之，斐波那契数列在数学、自然科学、经济学、艺术等领域都具有重要的理论价值和实际应用。